「背包問題」是計算機科學中經典的NP完全問題（非確定性圖靈機多項式複雜度求解的決定問題）之一，其相關研究長期以來備受科學家關注。

　記者27日從中國科學院金屬研究所獲悉，該所張志東研究員最近在計算機科學基礎理論領域取得一項突破性進展，首次精確確定了「背包問題」的計算複雜度下限，通俗而言就是發現計算速度極限。

　中國科學家破解「背包問題」複雜度之謎的這項基礎研究成果論文，近日在美國數學科學研究所出版社（AIMS）《數學》期刊發表。

　張志東研究員科普解讀說，「背包問題」假設你有一個容量有限的背包，面前擺著N件價值不同、重量各異的物品，如何選擇物品組合才能使總價值最大化？這個看似簡單的選擇問題，實則暗藏計算玄機：當物品數量超過一定規模後，即使使用最先進計算機也需要耗費天文數字時間求解，而「計算複雜度下限」就是解決問題所需的最少時間。

　在現實生活中，包括在物流運輸領域如何優化集裝箱裝載方案、在金融投資領域如何構建收益最大化的投資組合、材料科學領域如何尋找最優原子排列方式等，都涉及「背包問題」。

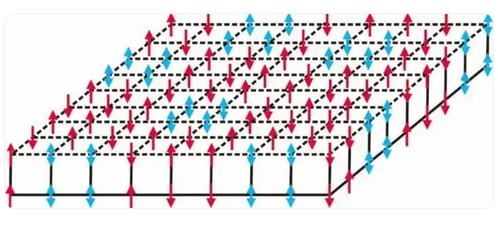
　中國科學院金屬研究所介紹，在10餘年三維伊辛模型研究工作的基礎上，張志東研究員此次建立起「背包問題」與自旋玻璃三維伊辛模型的聯繫，根據兩個問題的關係確定「背包問題」的計算複雜度的下限。

　他通過把每個物品的選擇（取或不取）對應為微觀粒子的兩種自旋狀態，將價值最大化問題轉化為尋找系統最低能量狀態，發現「絕對極小核心模型」，揭示計算複雜度的本源來自三維晶格中自旋排列的特殊拓撲結構。

　進一步通過構建計算複雜度相圖，張志東首次描繪出NP完全問題與NP中間問題的分界線，從而確定計算複雜度下限，證明最優算法的時間複雜度顯著優於現有算法。

　業內專家稱，「背包問題」可以被映射為許多其他科學問題，中國科學家此次破解其複雜度之謎的研究結論可直接推廣應用，助力解決計算機、物理、化學、生物、數學以及材料科學領域一系列相關基礎科學問題。（中新社記者 孫自法）

　圖：本項研究的自旋玻璃三維伊辛模型最小核模型示意圖，其中紅色自旋指向隨機分布，並且藍色自旋存在阻錯。中國科學院金屬研究所 供圖